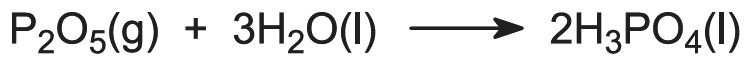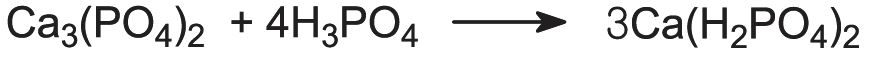Phosphorus is an essential plant nutrient and is taken up by plant roots, usually as the dihydrogenphosphate ion, H2PO4-, derived from phosphoric acid, H3PO4. The manufacture of fertilizers that are used to rectify phosphorus deficiencies in soils depends on the availability of supplies of phosphoric acid.
Uses of phosphoric acid
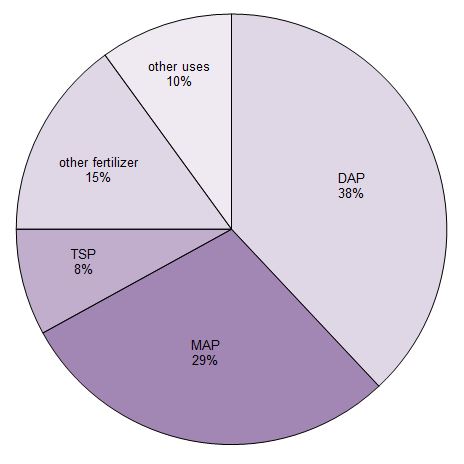
About 90% of the phosphoric acid produced is used to make fertilizers. It is mainly converted into three phosphate salts which are used as fertilizers. They are triple superphosphate (TSP), diamonium hydrogenphosphate (DAP) and monoammonium dihydrogenphosphate (MAP).
Figure 1 Uses of phosphoric acid.
Data from Potash Corporation, 2014
Phosphates are also used in a variety of other ways, including in soft drinks and as a supplement in feed given to cattle, pigs and poultry.
Although their use as builders in detergents has been phased out in many countries, it is still an important use for the acid in some countries.
Annual production of phosphoric acid
| World | 43 million tonnes1,2,3 |
| China | 17 million tonnes4 |
| South-east and north-east Asia (including Indonesia and Japan) |
10 million tonnes4 |
| US | 8.4 million tonnes5 |
1 Potash Corporation, 2014
2 JDCPhosphate, 2014
3 Estimate for 2016
4 Extrapolated from data, IHS,Markit, 2015
5 2015 Business of Chemistry, American Chemistry Council, 2016
Manufacture of phosphoric acid
Phosphoric acid is made by two processes:
a) the 'wet' process
b) thermal process
The thermal method normally produces a more concentrated and purer product, but is energy intensive (because of the manufacture of phosphorus itself. Acid produced by the 'wet' route is less pure but is used in the manufacture of fertilizers.
(a) Wet process
Phosphoric acid is produced from fluorapatite, known as phosphate rock, 3Ca3(PO4)2.CaF2, by the addition of concentrated (93%) sulfuric acid in a series of well-stirred reactors. This results in phosphoric acid and calcium sulfate (gypsum) plus other insoluble impurities. Water is added and the gypsum is removed by filtration along with other insoluble materials (e.g. silica). Fluoride, as H2SiF6, is removed at a further stage by evaporation.
Although the reaction takes place in stages involving calcium dihydrogenphosphate, the overall reaction can be represented as:
However, there are side reactions; for example with calcium fluoride and calcium carbonate present in the rock:
Fluorosilicilic acid is an important by-product from this and from the manufacture of hydrogen fluoride. It can be neutralised with sodium hydroxide to form sodium hexafluorosilicate. The acid is also used to make aluminium fluoride, used in turn in the manufacture of aluminium.
The crystal structure of the calcium sulfate formed depends on the conditions of the reaction. At 340-350 K, the principal product is dihydrate, CaSO4.2H2O. At 360-380 K, the hemihydrate is produced, CaSO4.1/2H2O.
Calcium sulfate is filtered off and the acid is then concentrated to ca 56% P2O5 using vacuum distillation.
The product from the 'wet process' acid is impure but can be used, without further purification, for fertilizer manufacture (see below). Alternatively it can be evaporated further to ca 70% P2O5, a solution called superphosphoric acid which is used directly as a liquid fertrilizer.
To make industrial phosphates, the acid is purified by solvent extraction using, for example, methyl isobutyl ketone (MIBK) in which the acid is slightly soluble and concentrated to give 60% P2O5 content. This acid can be further purified using solvents to extract it from heavy metals and defluorinated (by evaporation) to produce a product of food grade quality.
(b) Thermal process
The raw materials for this process are phosphorus and air:
Initially, phosphorus is sprayed into the furnace and is burnt in air at about 1800-3000 K.
Most processes use undried air and many involve the addition of steam to the phosphorus burner to produce and maintain a film of condensed polyphosphoric acids which protect the stainless steel burner tower (externally water cooled). The products from the burner tower pass directly into a hydration tower where the gaseous phosphorus oxide is absorbed in recycled phosphoric acid:
Alternatively, the phosphorus may be burnt in dried air. The phosphorus pentoxide is condensed as a white powder and separately hydrated to phosphoric acid.
This method allows heat to be recovered and reused.
Burning and direct hydration, as previously described, creates highly corrosive conditions. The equipment is constructed from stainless steel or is carbon brick-lined. To reduce corrosion, the walls of the burner and hydrator towers are cooled, but the reactor products emerge at a temperature too low for useful heat recovery.
The product acid has a concentration of ca 85%.
Tetraphosphoric acid, one of a family of polyphosphoric acids which can be selectively produced, is made either by boiling off water at high temperatures in a carbon vessel, or by adding solid phosphorus pentoxide to almost boiling phosphoric acid. The first method usually gives the purer product, due to the high arsenic content of phosphorus pentoxide.
Phosphates
The salts of phosphoric acid, the phosphates, are the compounds that are widely used in agriculture, industry and in the home.
(a) Ammonium phosphates
Monoammonium dihydrogenphosphate and diammonium hydrogenphosphate are much used as fertilizers and are made by mixing the correct proportions of phosphoric acid with anhydrous ammonia in a rotating drum.
The choice of which ammonium phosphate to use depends on the proportion of nitrogen and phosphorus needed for the crop.
(b) Calcium phosphates
The calcium phosphates are used extensively as fertilizers. Calcium dihydrogenphosphate, Ca(H2PO4)2, is produced by the reaction of phosphate rock with sulfuric acid:
This is known as superphosphate. It contains ca 20% P2O5.
If phosphate rock is treated with phosphoric acid, rather than sulfuric acid, a more concentrated form of calcium dihydrogenphosphate is produced with an overall higher P2O5 level (50%):
This is known as triple superphosphate. The higher level of phosphate is achieved because the product is no longer diluted with calcium sulfate.
(c) Sodium phosphates
Sodium phosphates are produced by reaction of phosphoric acid and a concentrated solution of sodium hydroxide in the appropriate (stoichiometric) proportions. The product crystallizes out.
- Monosodium dihydrogenphosphate (MSP, NaH2PO4) is used in metal cleaning and surface preparation formulations, as a source of phosphate in pharmaceutical manufacture, and as a pH control agent in toothpastes, in vitreous enamel coating (sanitary ware) and in the manufacture of starch phosphates. One of the biggest uses is as a plumbosolvency treatment in drinking water. Either phosphoric acid or MSP can be used to produce a thin insoluble coating of lead phosphate on lead pipes to prevent dissolution of the lead by the acids in the water.
- Disodium hydrogenphosphate (Na2HPO4) is used as a softening agent in processed cheese, in enamels and ceramic glazes, in leather tanning, in dye manufacture and as a corrosion inhibitor in water treatment.
- Trisodium phosphate (Na3PO4) is used in heavy-duty cleansers, for example in degreasing steel. It is an alkali and a sequestrant for calcium ions, keeping them in solution and preventing the formation of a scum.
- Disodium pyrophosphate (Na2H2P2O7) is used as a leavening agent in bread/cakes (it assists the liberation of carbon dioxide from baking soda), as an iron oxide suppressant (darkening or browning effect) in the manufacture of various foods and as a dispersant in oil-well drilling mud.
Date last amended: 5th January 2017